考研大纲包含了硕士研究生考试相应科目的考试形式、要求、范围、试卷结构等指导性考研用书。今天,为了方便2022考研的学子们,小编为大家整理了“2024考研大纲:重庆三峡学院2024年考研 005数学与统计学院 2.复试笔试科目概率论与数理统计 考试大纲”的相关内容,请持续关注!


以下为《005数学与统计学院 2.复试笔试科目概率论与数理统计》文档文字版,内容仅供参考,详情请下载文末附件查看:
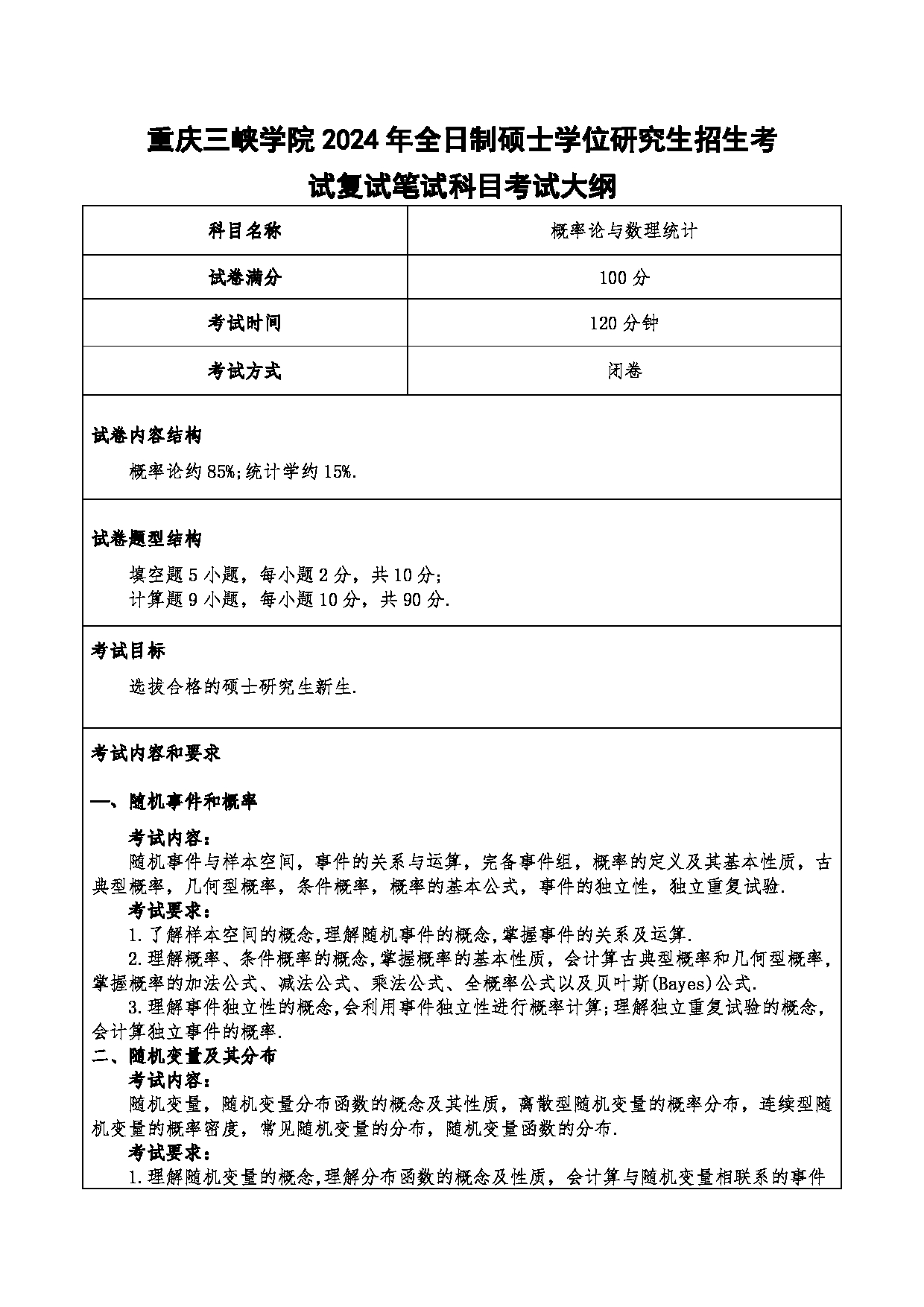
重庆三峡学院 2024 年全日制硕士学位研究生招生考
试复试笔试科目考试大纲
科目名称 概率论与数理统计
试卷满分 100 分
考试时间 120 分钟
考试方式 闭卷
试卷内容结构
概率论约 85%; 统计学约 15 %.
试卷题型结构
填空题 5小题,每小题 2分,共 10分 ;
计算题 9小题,每小题 10分,共 90分 .
考试目标
选拔合格的硕士研究生新生 .
考试内容和要求
— 、随机事件和概率
考试内容:
随机事件与样本空间 , 事件的关系与运算 , 完备事件组 , 概率的定义及其基本性质 , 古
典型概率,几何型概率,条件概率,概率的基本公式,事件的独立性,独立重复试验 .
考试要求:
1. 了解样本空间的概念 ,理解随机事件的概念 ,掌握事件的关系及运算 .
2.理解概率 、 条件概率的概念 ,掌握概率的基本性质 , 会计算古典型概率和几何型概率 ,
掌握概率的加法公式、减法公式、乘法公式、全概率公式以及贝叶斯 (Bayes) 公式 .
3. 理解事件独立性的概念 ,会利用事件独立性进行概率计算 ;理解独立重复试验的概念 ,
会计算独立事件的概率 .
二、随机变量及其分布
考试内容:
随机变量 , 随机变量分布函数的概念及其性质 , 离散型随机变量的概率分布 , 连续型随
机变量的概率密度,常见随机变量的分布,随机变量函数的分布 .
考试要求:
1. 理解随机变量的概念 ,理解分布函数的概念及性质,会计算与随机变量相联系的事件
的概率 .
2.理解离散型随机变量及其概率分布的概念 ,掌握 0-1 分布、二项分布、几何分布、泊
松 (Poisson) 分布及其应用 .
3. 了解泊松定理的结论和应用条件 ,会用泊松分布近似表示二项分布 .
4.理解连续型随机变量及其概率密度的概念,掌握均匀分布、正态分布、指数分布及
其应用 .
5.会求随机变量函数的分布 .
三、多维随机变量及其分布
考试内容:
多维随机变量及其分布 , 二维离散型随机变量的概率分布 、 边缘分布和条件分布 , 二维
连续型随机变量的概率密度和边缘概率密度 , 随机变量的独立性和不相关性 , 常用二维随机
变量的分布 .
考试要求:
1.了解多维随机变量的概念 ,了解多维随机变量的分布的概念和性质,理解二维离散型
随机变量的概率分布 、 边缘分布和条件分布 , 理解二维连续型随机变量的概率密度 、 边缘密
度和条件密度 ,会求与二维随机变量相关事件的概率 .
2. 理解随机变量的独立性及不相关性的概念 ,掌握随机变量相互独立的条件.
3. 掌握二维均匀分布,了解二维正态分布的概率密度,理解其中参数的概率意义 .
4. 会求两个随机变量简单函数的分布 ,会求多个相互独立随机变量简单函数的分布 .
四、随机变量的数字特征
考试内容:
随机变量的数学期望 (均值 )、方差、标准差及其性质,随机变量函数的数学期望,矩 、
协方差、相关系数及其性质 .
考试要求:
1. 理解随机变量数字特征 ( 数学期望 、 方差 、 标准差 、 矩 、 协方差 、 相关系数 ) 的概念 ,
会运用数字特征的基本性质 ,并掌握常用分布的数字特征 .
2. 会求随机变量函数的数学期望.
五、大数定律和中心极限定理
考试内容:
切比雪夫不等式,切比雪夫大数定律,伯努利大数定律,辛钦大数定律,棣莫弗 -拉普
拉斯定理,列维 -林德伯格定理 .
考试要求:
1. 了解切比雪夫不等式 .
2. 了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律 (独立同分布随机变量序列
的大数定律 ).
3. 了解棣莫弗 -拉普拉斯定理 (二项分布以正态分布为极限分布 )和列维 -林德伯格定理
(独立同分布随机变量序列的中心极限定理 ).
六、数理统计的基本概念
考试内容:
总体个体 , 简单随机样本统计量 , 样本均值 、 样本方差和样本矩 , 卡方分布 、 t分布 、 F
分布,分位数,正态总体的常用抽样分布 .
考试要求:
1. 理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念 .
2. 了解卡方分布、 t分布和 F分布的概念及性质,了解上侧 α 分位数的概念并会查表计
算 .
3. 了解正态总体的常用抽样分布 .
七、参数估计
考试内容:
点估计的概念 , 估计量与估计值 , 矩估计法 , 最大似然估计法 , 估计量的评选标准 , 区
间估计的概念,单个正态总体的均值和方差的区间估计 .
考试要求:
1. 理解参数的点估计、估计量与估计值的概念 .
2. 掌握矩估计法 (一阶矩、二阶矩 )和最大似然估计法 .
3. 了解估计量的无偏性、有效性 (最小方差性 )和一致性 (相合性 )的概念 ,并会验证估计
量的无偏性 .
4. 理解区间估计的概念 ,会求单个正态总体的均值和方差的置信区间 .
八、假设检验
考试内容:
显著性检验,假设检验的两类错误,单个及两个正态总体的均值和方差的假设检验 .
考试要求:
1. 理解显著性检验的基本思想 ,掌握假设检验的基本步骤 ,了解假设检验可能产生的两
类错误 .
2. 掌握单个及两个正态总体的 t均值和方差的假设检验 .
参考书目
(1) 盛骤 ,谢式千 ,潘承毅 .概率论与数理统计 [M]. 北京:高等教育出版社, 2020.
(2) 陈希孺 .概率论与数理统计 [M]. 合肥:中国科学技术大学出版社, 20 09.
(3) 曹显兵 ,莫立坡 ,梁新刚 .概率论与数理统计 [M]. 北京:中国人民大学出版社, 2021.
备注
以上就是小编整理的“2024考研大纲:重庆三峡学院2024年考研 005数学与统计学院 2.复试笔试科目概率论与数理统计 考试大纲”的全部内容,更多关于重庆三峡学院2024年考研大纲的信息,尽在“考研大纲”栏目,定会对大家有所帮助!



