考研大纲包含了硕士研究生考试相应科目的考试形式、要求、范围、试卷结构等指导性考研用书。今天,为了方便2022考研的学子们,小编为大家整理了“2024考研大纲:重庆三峡学院2024年考研 005数学与统计学院 2.复试笔试科目常微分方程 考试大纲”的相关内容,祝您考研顺利!


以下为《005数学与统计学院 2.复试笔试科目常微分方程》文档文字版,内容仅供参考,详情请下载文末附件查看:
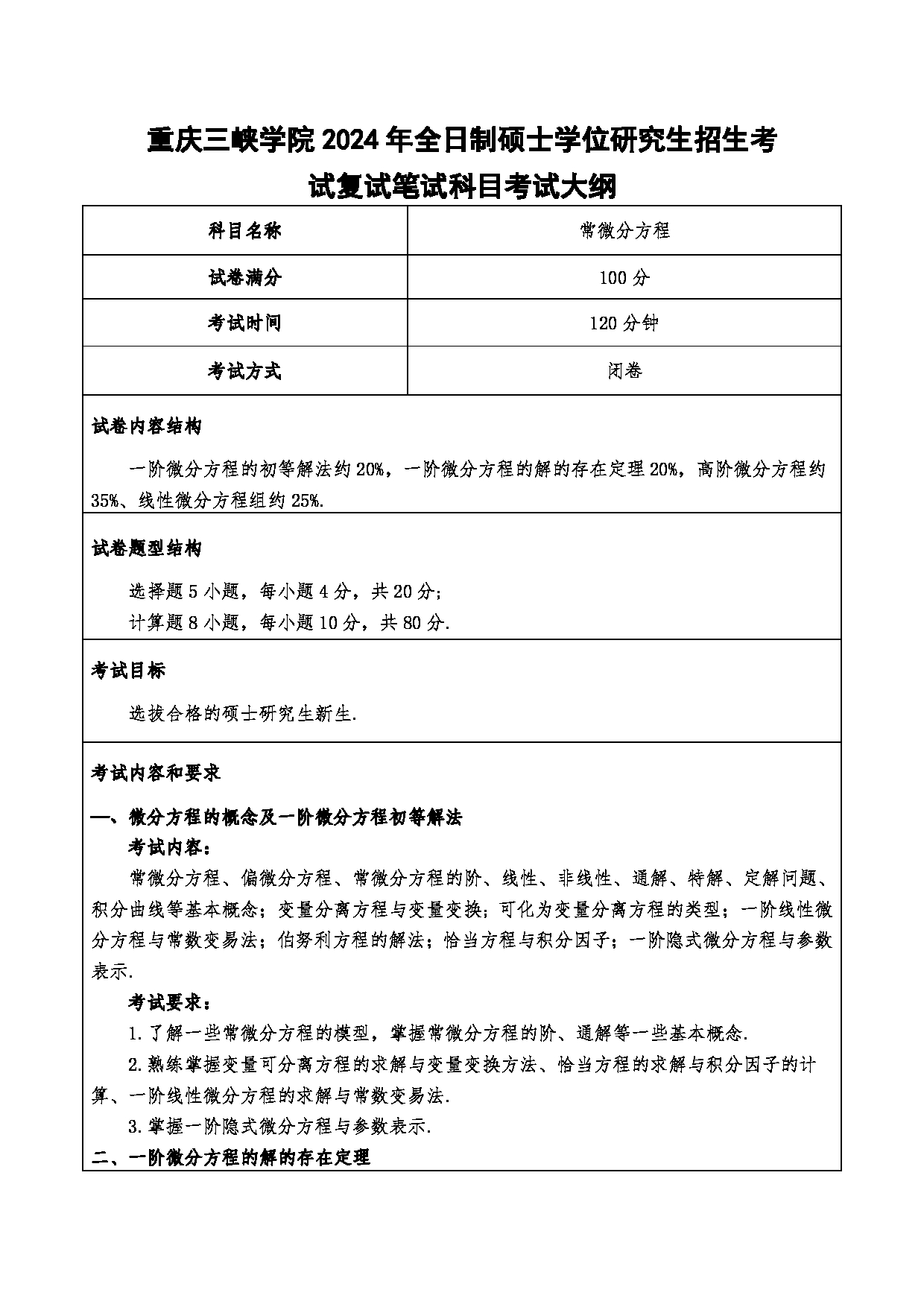
重庆三峡学院 2024 年全日制硕士学位研究生招生考
试复试笔试科目考试大纲
科目名称 常微分方程
试卷满分 100 分
考试时间 120 分钟
考试方式 闭卷
试卷内容结构
一阶微分方程的初等解法约 20% ,一阶微分方程的解的存在定理 20% ,高阶微分方程 约
35% 、线性微分方程组 约 25 %.
试卷题型结构
选择题 5小题,每小题 4分,共 20 分 ;
计算题 8小题,每小题 10分,共 80 分 .
考试目标
选拔合格的硕士研究生新生 .
考试内容和要求
— 、微分方程的概念及一阶微分方程初等解法
考试内容:
常微分方程、偏微分方程、常微分方程的阶、线性、非线性、通解、特解、定解问题 、
积分曲线等基本概念 ; 变量分离方程与变量变换 ; 可化为变量分离方程的类型 ; 一阶线性微
分方程与常数变易法 ; 伯努利方程的解法 ; 恰当方程与积分因子 ; 一阶隐式微分方程与参数
表示 .
考试要求:
1. 了解 一些常微分方程的模型 ,掌握 常微分方程的阶、通解等一些基本概念 .
2.熟练掌握 变量可分离方程的求解与变量变换方法、恰当方程的求解与积分因子的计
算、 一阶线性微分方程的求解与常数变易法 .
3. 掌握一阶隐式微分方程与参数表示 .
二、一阶微分方程的解的存在定理
考试内容:
解的存在唯一性定理与逐步逼近法;近似计算和误差估计;解的延拓,解的延拓定理 ,
解关于初值的对称性定理、解对初值的连续依赖性定理、解对初值的可微性定理 .
考试要求:
1. 了解解的延拓定理、解对初值的连续性 、 依赖性和可微性定理 .
2. 掌握解的存在唯一性定理、皮卡逐步逼近法、方程的近似解和误差估计 .
三、高阶微分方程
考试内容:
线性微分方程的一般理论: n阶(非)齐次线性方程的概念, n阶线性方程的解的存在
唯一性定理的条件、结论,叠加原理,函数线性相关、线性无关的概念,函数组的 Wronsk y
行列式,利用 Wronsky 行列式判定线性方程的解的线性关系, n阶齐次线性方程通解结构定
理,基本解组的概念, n阶非齐次线性方程的解的性质和通解结构; n阶非齐次线性方程的
常数变易法 ; 常系数线性方程的解法 , 复值函数与复值解的概念和性质 , 运用复数法求解非
齐次线性微分方程的特解 ; 常系数齐次线性微分方程的基本解组的特征根法 ; 用比较系数法
求解非齐次线性微分方程的特解 ; 欧拉方程的求解 , 用拉普拉斯变换法求解非齐次线性微分
方程的特解;高阶微分方程的降阶和幂级数解法 .
考试要求:
1.了解 复值函数与复值解的概念和性质,拉普拉斯变换法 .
2. 掌握 高阶线性微分方程的理论,解的性质与结构 .
3.熟练掌 握 n阶非齐次线性方程的常数变易法 , 常系数齐次线性微分方程和欧拉方程的
求解 , 非齐次线性微分方程和比较系数法 ,可降阶的一些方程类型 ( 不显含未知数 x, 自变 量
t)的解法 .
四、线性微分方程组
考试内容:
存在唯一性定理;齐次线性微分方程组,叠加原理, Wronsky 行列式,向量函数的线性
相关 、 无关与 Wronsky 行列式的关系 ; 基本解组 , 齐次线性方程组的通解结构 , 解结构理论
的矩阵表述,非齐次线性方程组的通解结构; n阶非齐次线性方程组的常数变易公式;常系
数性微分方程组,矩阵指数 expA 的定义和性质;基解矩阵的计算公式 .
考试要求:
1. 了解存在唯一性定理 .
2. 掌握线性微分方程组的通解结构 , 齐次线性微分方程组的基解矩阵概念 , 非齐次线性
方程组的常数变易法 .
3.掌握矩阵指数 expA 的定义和性质 .
4. 熟练掌握基解矩阵的计算公式 .
参考书目
1. 王高雄等,常微分方程 (第三版 ),北京:高等教育出版社, 2006.
2. 伍卓群、李勇,常微分方程,北京:高等教育出版社, 2004.
3. 东北师范大学微分方程教研室 , 常微分方程 (第二版 ), 北京 : 高等教育出版社 , 2005.
4.叶彦谦等,常微分方程讲义 (第二版 ),北京:人民教育出版社, 1979.
5.丁同仁,李承治 ,常微分方程 (第二版 ),北京:高等教育出版社, 2004.
6.张伟年,杜正东,常微分方程 (第二版 ),北京:高等教育出版社, 2014
备注
以上就是小编整理的“2024考研大纲:重庆三峡学院2024年考研 005数学与统计学院 2.复试笔试科目常微分方程 考试大纲”的全部内容,更多关于重庆三峡学院2024年考研大纲的信息,尽在“考研大纲”栏目,下面我们一起来看看吧!



